이전 포스트에서 e라는 상수에 대해 얘기했었다.
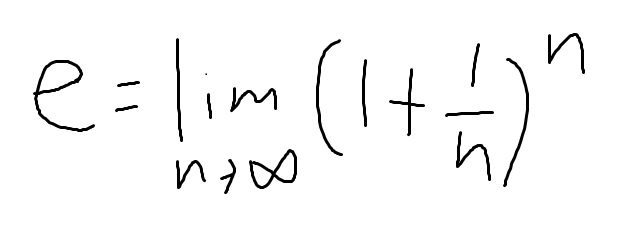
여기서 n 은 자연수였다.
그런데, n이 실수여도 무한대로 가는 건 마찬가지이니,
실수 범위에서 적용해도 결과는 같을 것이다.
그래서

이렇게도 가능하고,
1/r 은 0에 다가가므로,

이렇게도 표현할 수 있다.
이 형태를 잘 기억하기 바란다.
지수함수 미분시, 이런 형식을 만들어 치환시키면서 유도할 것이기 때문이다.
지수함수란건 미지수 x가 있을 때,

이런 형식이다. a는 임의의 양의 실수로 하겠다.
0이나 음의 실수는 정의역에 따라 실수로 나타나지 않거나 정의할 수 없기 때문이다.
그러면 상수 e 에 대해서도 지수함수를 만들 수 있을 것이다.
그리고 이 함수를 미분하도록 하겠다.
일단 이 함수가 연속임을 알아보자.
e^x 는 e가 2와 3 사이에 있는 양수이므로,
정의역이 실수일 때, 정의역의 모든 원소에서 치역이 존재하며,
임의의 원소 x=c에서 전개하면,

e^x 의 극한이 존재하므로 e^x 는 일단 연속함수이다.
이제, 도함수의 좌 우 극한이 일치하는지 보자.
우선 0보다 큰 임의의 상수 c에서 e에 대한 로그 함수인 ln x 가 연속하는지를 보겠다.

0보다 큰 임의의 상수 c에 대해 ln(x) 가 연속함을 보였다.
이를 이용하여 임의의 상수 c에 대한 도함수를 구해보자.
실수인 임의의 상수 c에 대해서 보면,

c에서 미지수 x를 붙이면 e^x이고,
이 함수는 위에서 봤듯이 모든 실수에서 연속이므로,
e^x의 도함수는 e^x라고 할 수 있다.
e^x를 보니, 미분을 해도 같은 결과가 나온다는 것을 알 수 있다.
그렇기 때문에 미적분과 관련해서 많이 이용되는 함수이다.
마저 지수함수에 대한 미분을 알아보자

이렇게 된다.
'교육 > 수알못시리즈' 카테고리의 다른 글
| 삼각함수의 덧셈 합성 Additive synthesis of trigonometric functions (0) | 2020.04.19 |
|---|---|
| 삼각함수의 미분 Differential of trigonometric function (0) | 2020.04.19 |
| 삼각함수와 지수함수의 테일러 급수 Taylor series of trigonometric and exponential function (0) | 2020.04.19 |
| 테일러 급수 Taylor series (0) | 2020.04.16 |
| 미분과 적분과의 관계 Relation between differential and integral (0) | 2020.04.13 |



