이전 포스트에서 함수값의 변화를 통해 미분, 도함수를 이끌어냈었다.

그러면, 미분 가능한 함수에서

이런 관계가 성립되는지가 궁금할 것이다.
이게 성립한다고 하면, 이 정리를 평균값 정리라고 할 것이다.
일단, f가 x와 x+Δx 구간에서 1차 다항 함수이면,
해당 구간에서 도함수는 이런 식으로 되므로,
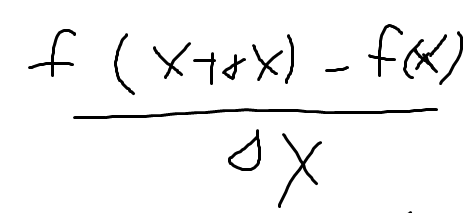
위 식이 성립된다.
해당 함수가 1차 다항 함수가 아닌 일반적인 경우를 생각해보자.
이 경우는 조금 복잡하게 생각해야하기 때문에
다른 정리를 통해서 앞에서 파악하고자하는 사실을 증명해보겠다.
그렇기에 우선 다른 정리라고 하는 것을 소개하고 왜 그렇게 되는지를 보이겠다.
다른 정리라고 하는 거는 롤의 정리라고 이름하기도 하는데,
정리의 내용은 다음과 같다.

a의 함수값과 b의 함수값이 같을 때, a, b 사이에 있는 p 함수값이 있어
p의 도함수 값은 a와 b 사이의 기울기인 0과 같다는 얘기다.
p의 함수값이 구간 내에서 최소일 때도 같은 방식으로 보일 수 있다.
이 정리로써 평균값 정리를 마저 증명하도록 하겠다.

이런 식이 된다.
모든 정의역에서 미분 가능한 함수가 있다면,
임의의 x에 대해 다음이 성립한다는 얘기이고,

도함수의 극한을 다른 방식으로 표현할 수 있는 근거가 된다.
'교육 > 수알못시리즈' 카테고리의 다른 글
| 부정적분 Indefinite integral (0) | 2020.04.13 |
|---|---|
| 함수 덧셈에 관한 리만 적분 Riemann integral about addition of functions (0) | 2020.04.13 |
| 도함수/미분 Derivative (0) | 2020.04.13 |
| 푸비니 정리 Fubini theorem (0) | 2020.04.13 |
| 리만 적분 Riemann integral (0) | 2020.04.05 |



