인류가 세상을 편하게 살기위해
시간에 따른 변화를 파악하면서 분석하고 예측을 했었다.
특히, 속도, 가속도 같은 것들을 파악하면서
물체의 움직임에 대해 명확하게 파악할 수 있었고,
덕분에 과학의 발전 정도가 상당히 증가했다.
앞에 서술 했던 사항을 조금 더 일반화 하면 다음과 같이 얘기할 수 있을 것이다.
정의역 변화에 따라 함수값 변화가 있을 것인데,
이걸 그래프 상으로 그렸을 때는 기울기라고 한다.
식으로 나타내면 다음과 같은 식이다.
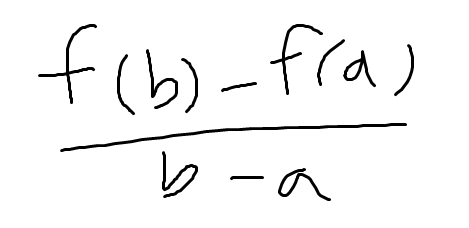
만약에 정의역 구간을 한 없이 좁혔을 때를 생각해보자.
b를 a에 한없이 가까이 접근 시켰을 때를 얘기하면,

이렇게 나타낼 수 있을 것이다.
이걸 다른 말로해서 a에서의 미분이라고도 얘기한다.
여기에서 조건을 붙이면, a가 개구간 I 에 있고, 구간 I에 있는 임의의 원소 b로 정하면 될 것이다.
위 식에서 b부분이 a에 다가간다는 거는 b가 미지수라는 얘기인데,
보통 미지수를 쓸 때, x가 더 익숙하므로,
b부분을 x로 바꿔서 정리하면,

이런 식으로 표현할 수 있을 것이다.
x를 집어넣은 버전의 a의 미분 표현이다.
위 식에서 a 대신 미지수 x 를 넣고,
x자리 대신에 y를 넣어서 표현하면,

이런 식이 되고, 미지수 x에 대한 미분이라고 하는데,
미지수이기 때문에 함수 f(x)의 도함수라고 얘기를 한다.
도함수가 있을 때, 특정값 a를 넣으면
아까 얘기한대로 a에서의 미분이라고도 하지만,
a에서의 미분계수라고도 한다.
D f(x) 는 도함수, 여기에 x=a 대입해서 D f(a)는 a에서의 미분계수 이런 식이다.
이 식을 보면 극한으로 표현되었으므로,
극한에 있는 특성으로 얘기할 수 있는 것이 있을 것이다.
도함수의 좌극한이니 우극한이니 하는 것들 말이다.
이걸 좌 미분계수, 우 미분계수라고도 한다.
이 지표들은 함수가 미분 가능 여부를 파악하는 중요한 것들이라 할 수 있겠다.
미분 가능이란 말이 나와서 그런데,
미분 가능한 조건을 얘기해보겠다.
연속적인 변화에 대해서 순간적인 변화의 정도를 파악하는 것이므로,
일단 연속함수에서 정의가 될 것이다.
여기서 특정 지점에서 좌 미분계수와 우 미분계수가 같다는 조건을 더 붙이면,
이 함수는 해당 지점에서 미분 가능한 함수로 정할 수 있을 것이다.
서술한 조건을 정리하면,

이런 식이다.
미분 가능한 함수에 대해서 함수의 사칙연산이 어떻게 작용되는지 보자.




이런 식으로 되고,
합성함수에 대해서는

이렇게 된다.
'교육 > 수알못시리즈' 카테고리의 다른 글
| 함수 덧셈에 관한 리만 적분 Riemann integral about addition of functions (0) | 2020.04.13 |
|---|---|
| 평균값 정리 Mean value theorem (0) | 2020.04.13 |
| 푸비니 정리 Fubini theorem (0) | 2020.04.13 |
| 리만 적분 Riemann integral (0) | 2020.04.05 |
| 함수의 연속 Continuity of a function (0) | 2020.04.02 |



