어떤 도형의 넓이를 구할 때 기본 단위는 직사각형의 넓이이다.
다차원 영역에서 영역의 크기를 얘기할 수도 있지만,
가장 쉽게 인식할 수 있는 게 넓이이므로 여기에 대해 얘기를 시작하도록 하겠다.
넓이의 기본이 직사각형의 넓이이니까
여러 복잡한 도형의 넓이도 직사각형 기준으로 파악할 수 있을 것이다.
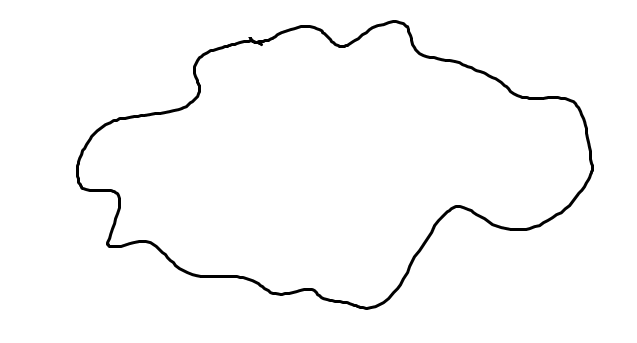
이런 도형이 있다고 할 때,

이런 식으로 직사각형을 그려서 도형의 넓이를 근사할 수 있다.
근사할 순 있지만 차이는 있다.
근사하는 기준이 각 범위 내에서 최대값을 기준으로 근사할 수도 있고,
최소값을 기준으로 근사할 수도 있다.
이 두 기준으로 구한 값은 차이가 있을 수 밖에 없다.
이 둘의 차이를 줄이면, 아무래도 더 도형의 넓이를 정확하게 구할 수 있을 것이다.
이를 위해서 각 영역에 있는 값에 대한 간단한 생각으로 부터
최대값, 최소값의 차이를 어떻게 좁힐 지 파악해보자.

영역 A와 B가 있을 때 A는 B의 부분 영역이 된다.
각 영역에 값이 정해질 때,
B 영역의 최대 혹은 최소값은 A영역 밖에 있을 수도 있고,
A영역 안에 있을 수도 있다.
B의 최대 혹은 최소값이 A 영역안에 있으면,
A의 최대 혹은 최소값도 B의 최대 혹은 최소값과 같다.
하지만 B의 최대 혹은 최소값이 A 영역 밖에 있으면,
최대값일 경우는 B의 최대값이 A의 최대값보다 클 것이고,
최소값일 경우 B의 최소값은 A의 최소값보다 작을 것이다.
따라서, B의 최대값은 A의 최대값보다 크거나 같으며,
B의 최소값은 A의 최소값보다 작거나 같음을 알 수 있다.
값을 f : B -> R 로 나타낸다고 하고,
B 영역에서의 최대값, 최소값을 다음과 같이 정의한다고 하면,

크기 관계는 다음과 같이 될 것이다.

이건 무엇을 의미하겠는가?
집합 범위를 좁게 잡을수록 최대값 최소값의 차이가 적어짐을 의미한다.

즉, 여기서 더 잘게 쪼개면 더 근사한 수치로 이 도형의 넓이를 구할 수 있다는 얘기다.
이를 명확한 형식으로 나타내보도록 하자.
우선, 기준 좌표축을 그리고, 시작점과 끝점을 잡아 범위를 잡을 수 있을 것이다.
그리고 각 지점에 대한 도형의 수직길이 함수를 정할 수 있을 것이다.

이렇게 a에서 b까지 n개로 나누고 나눈 범위에서 길이의 최대값과 범위의 길이를 곱해서 다 더해주고,
길이의 최소갑과 범위의 길이를 곱해서 다 더해서 도형의 넓이를 근사할 수 있다.
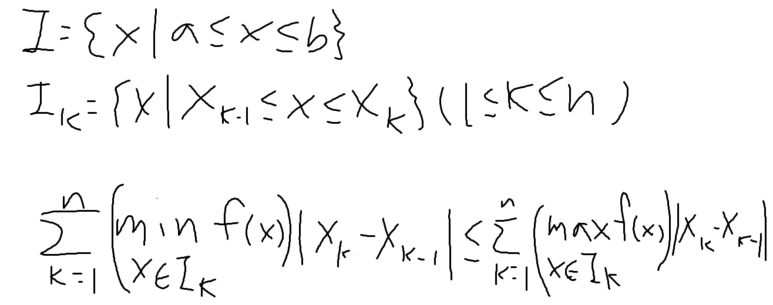
f(x)는 x 지점에서의 수직 길이가 된다.
1=< k =< n 에서 각 I_k 범위를 잘게 쪼개어 보자.

이런 식으로 될 것이고,
전체 I 구간에서는

이런 양상이 될 것이고,
새로이 잘라놓은 구간의 갯수는
물론 l(k)가 1보다 큰 자연수라고 하면, n개보다 더 많이 갈랐다는 사실을 알 수 있고,


세분하게 범위를 갈라 직사각형을 만들어 더한 값을 넓이로 정할수록
구하고자하는 도형의 넓이에 근사한다는 사실을 알 수 있다.
그리고 이는

이러므로,

한없이 가르면 도형의 넓이를 파악할 수 있다는 얘기가 된다.
이걸 조금 더 간단히 나타내면
n이 무한대로 갈 때 I_k 가 0으로 가므로, 이걸 dx라고 하고 나타내면,

이렇게 나타낼 수 있을 것이고,
이게 도형의 정확한 넓이가 될 것이다.
이런 개념을 일반 함수에도 이런 걸 적용할 수 있을 것인데,
잘게 쪼개서 최대값, 최소값 격차를 한 없이 줄일 수 있다면,
이런 방식의 연산을 적분 중에서도 리만 적분이라고 한다.
리만 적분이라고 따로 부르는 이유는 위에 전개한 방식으로 적용이 되지 않는 함수가 있기 때문에
그런 거하고 구분하기 위해서 부른다.
고등학교 때 유도했던 방식이 리만 적분의 유도이다.
일단 상수곱을 하면, 적분 값도 상수곱이 된다.
상수값을 넣었을 때, 상수는 합 기호나 극한 기호에 영향을 받지 않기 때문이다.
덧셈은

이런 논리를 적용할 수 있을 것이다.
도형의 넓이에 대한 예시를 들었지만,
리만 적분이 되는 함수에 대해서도 충분히 적용할 수 있다.
여기에서

a에서의 길이는 있겠지만, 간격은 0이므로 넓이는 0이 되는 것이 맞다.
이것도 역시 리만 적분에 적용할 수 있다.
그러면, 여기서 덧셈에 대한 정리와 바로 위의 사실을 토대로

위 아래 적는 순서가 바뀌면 부호가 바뀐다는 사실을 도출해낼 수 있다.
정리하면, 다음과 같다.


'교육 > 수알못시리즈' 카테고리의 다른 글
| 도함수/미분 Derivative (0) | 2020.04.13 |
|---|---|
| 푸비니 정리 Fubini theorem (0) | 2020.04.13 |
| 함수의 연속 Continuity of a function (0) | 2020.04.02 |
| 함수의 극한 limit of a function (0) | 2020.04.02 |
| 등차수열과 등비수열의 합 Summation of arithmetic progression and geometric sequence (0) | 2020.04.01 |



