함수의 극한과 함수의 연속은 긴밀한 관계에 있다.
통상적으로 함수는 실수 집합 혹은 그와 대등한 집합 내에서 설명이 되므로,
함수의 연속은 실수의 완비성과도 연관있다고 보면 된다.
연속이 된다는 게 기하학 적으로 보면 선으로 쭉 이어진다는 얘기 아닌가?
그래서 함수 간격에 대해 얘기한 함수의 극한 개념이 필요하고,
정의역의 해당 원소에서의 함수 값이 존재해야 하기도 하다.
그렇기 때문에 함수의 연속 조건은 다음과 같다.
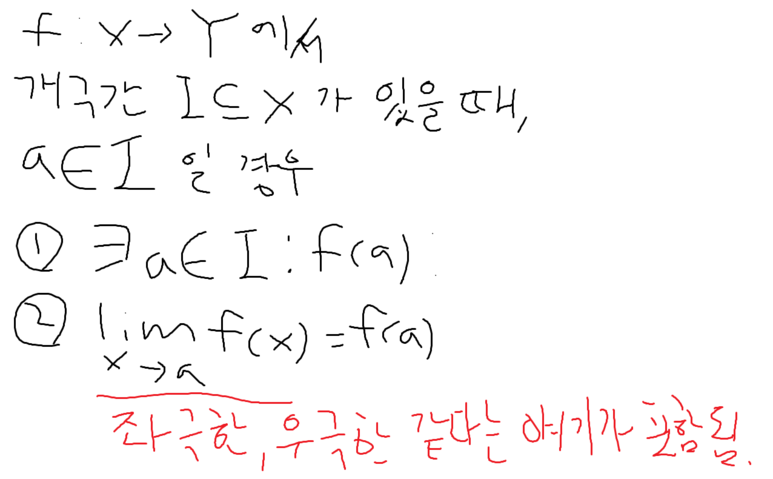
이 조건이 성립되면 함수는 x = a 에서 연속한다고 한다.
세 가지 조건으로도 얘기하는데,
2번 조건을 두개로 나눠서
좌극한, 우극한 같은 조건 하나,
이 두 극한이 x =a 에서의 함수값과 일치해야하는 조건 하나로 분리해서 그런 것이다.
그림으로 그리면,

이런 식이다.
이해하기 쉽도록 한 것이니 이 그림에만 매도되어 편견을 가지지 말고
참고 정도만 하면 될 것이고 다른 경우들도 충분히 생각해서 편견을 가지지 않도록 조심하면 좋겠다.
함수에 연속에 대해서 얘기했으니,
합성 함수에 대한 연속도 얘기할 수 있을 것이다.

이런 식으로 말이다.
빨간 부분은 함수가 해당 지점에서 연속이기 때문에 가능한 설정이다.
합성 함수에서 해당 지점과 해당 지점의 함수 값에서 연속이면,
합성 함수가 연속이라는 얘기다.
즉, 해당 지점에서의 연속과 함수 값에서의 연속 여부를 다 따져봐야 한다는 뜻이다.
연속 함수에서는 이런 가정도 가능할 것이다.
a < c < b 가 있어, f(a) < f(b) 일 때,
f(a) < u < f(b) 인 u = f(c) 가 되는 c 가 존재한다.
f(a) > f(b) 일 때, f(b) < u < f(a) 인 u = f(c) 가 되는 c가 존재한다는 것 까지 포함해서
중간값 정리라고 하는데,
f(a) < f(b) 인 경우만 보이면, 나머지 한 경우는 반대로 증명하면 되므로,
전자의 경우만 보이겠다.

여기서 S는 f(a)<u 이므로, a가 S에 속하므로, S는 공집합이 아니다.
나머지 한 쪽 측면을 마저 살펴보도록 하자.

이렇게 중간값 정리가 성립함을 보였다.
'교육 > 수알못시리즈' 카테고리의 다른 글
| 푸비니 정리 Fubini theorem (0) | 2020.04.13 |
|---|---|
| 리만 적분 Riemann integral (0) | 2020.04.05 |
| 함수의 극한 limit of a function (0) | 2020.04.02 |
| 등차수열과 등비수열의 합 Summation of arithmetic progression and geometric sequence (0) | 2020.04.01 |
| 상수 e The constant e (0) | 2020.03.31 |



