이 상수가 나온 경위는 은행에서 적금을 드는 경우에서 비롯되었다고 한다.
실제 은행 적금 제도가 복잡하긴 하겠지만, 단순하게 생각해보겠다.
단순하게 아무런 제재 없이 아무리 짧은 기간이라도 적금들고 이자받고 다시 적금할 수 있다하면,
일정기간 동안 자기가 넣은 금액이 적금들었다 빼고 다시든 횟수에 따라 어떻게 될 지 궁금할 것이다.
쉽게, 말이 안되지만, 1년 이자율 100%인 적금이 있다고 하자.
이 적금은 기간에 비례해서 적금 이율이 있고, 마음대로 기간을 정할 수 있다고 해보겠다.
1년에 2번 씩 6개월 적금 두 번 들 수도 있고,
3번 씩 4개월 적금 세 번 둘 수도 있는 식이다.
이 때, 1만큼을 1년 적금 들었다고 하자.
그러면, 1에다가 이자율 100 프로니까 1만큼의 이자가 더 생겨 1년 후에는 2만큼이 된다.
그러면, 6개월 씩 2번 적금을 둔 다고 생각해보자.
6개월이니까 기간 비례해서 1년의 반이니 50% 이율이다.
이런 적금에 아까와 같이 1만큼 적금 들었다 생각해보자.
6개월 후에는 1에 0.5만큼의 이자가 생겨서 총 1.5가 내 돈이 된다.
한 번 더 6개월 짜리 적금을 든다 생각하면,
1.5의 돈을 넣고 6개월을 기다리게 되는 것이니,
1.5에서 절반인 0.75만큼 이자가 생기므로 총 2.25가 내 돈이 된다.
쌩 1년 적금 든 거보다 내 돈이 더 많게 됐다.
이런 식으로 1을 투입해서 3번 적금 한 거는 계산해보면 1년 후 내 돈이 2.37이 된다.
적금 횟수가 많아지면 내 돈이 더 많이지는 거 같다.
일단, n 번 적금 했을 때, 1년 후의 내 돈은 얼마인지 보면,

빨간색 밑줄 친 것이 1년 후 내 돈이 된다.
그러면, 일정 기간 내에 적금 횟수가 많아질수록 최종적으로 내 돈이 많아지는지 알아보자.


n^2 + n - 1 부분은 ( n + 1/2 ) ^2 - 5/4 이고,
n을 실수로 볼 때 그림은

이런 식이고, n은 1보다 크거나 같은 자연수이므로,
n = 1 일 때가 가장 작음을 알 수 있다.
n = 1 일 때, 값은 1 이므로,
n^2 + n + 1 은 모든 자연수에 대해 0보다 크고,
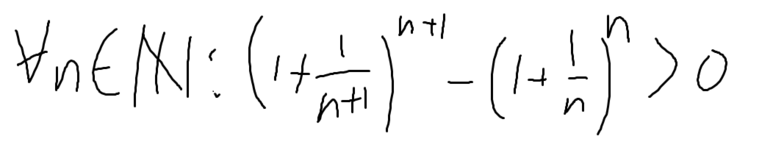
따라서 모든 자연수에 대해 위 식이 0보다 크다.
그런 즉, 일정 기간 내 적금 횟수가 많아질수록 일정 기간 후 내 돈이 많아진다.
n 이 클수록 커지니 말이다.
그러면,

이 값이 한 없이 커질지 궁금하다.
알다시피 자연수 범위에서 최소값은 2이다.
최대값이 있을지 없을지 파악해보자.
일단 위의 식을 전개하도록 하자.
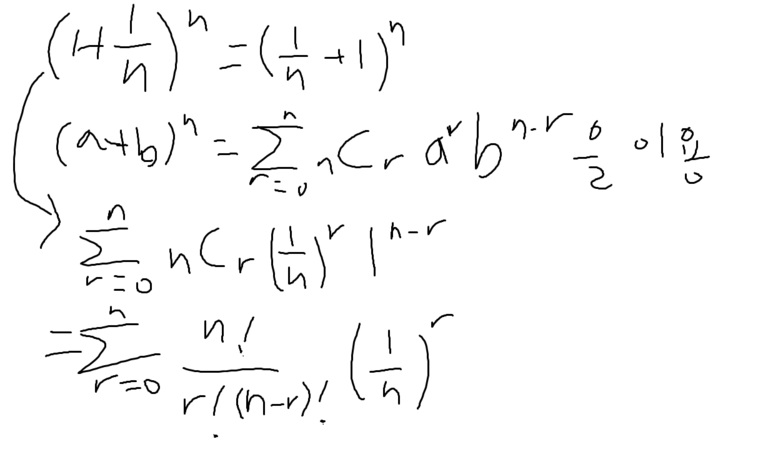
일단 이렇게 전개할 수 있겠고,
시그마 안에 있는 걸 파악하면,

두 번째 식에서 r은 0이 아니고, 자연수일 때이다.
여기서 1/n 도 r개 곱했으므로,
괄호안에 넣어서 다음과 같이 표현할 수 있다.

그러면, 처음 식은

이렇게 전개할 수 있다.
여기서 n이 무한대로 갈 때 값이 위 식의 극한이므로,
무한대로 보내보자.
k 는 상수이므로, r번째 항은

이런 식으로 될 것이고,
마지막 항을 보게되면,


결국 마지막 항은 무한대로 보낼 때 무시해도 된다.
그러므로,

식은 이런 식으로 나타낼 수 있다.
그러면 이 값이 한 없이 커지는 지 알아보자.
우선, 한 가지 사실을 알아보자.

이 사실로 부터

이런 식을 이끌어낼 수 있고,
( r > 1 어야 한다. )
이것의 값은 유한한 값을 가진 유한한 항들의 덧셈이므로,
유한한 값임을 알 수 있다.
즉, 일정 기간 내에 아무리 적금 횟수를 늘려봐야 일정 기간 내에 받을 돈은 유한하다는 얘기다.
유한한 값은 특정 기호로 나타낼 수 있을 것이다.
b( Bernoulli 베르누이의 첫 글자)인 적도 있다고 하는데, 최종적으로는 e라고 정했다.
오일러(Euler)라는 사람이 이 수에 대한 공이 커서
이 사람 이름의 첫 글자인 e라고 정한 모양이다.
이 수가 특정한 수임을 알았으니,
이 수가 유리수인지 무리수인지 알아보자.

e는 어떤 상수이며, 무리수 인 것까지 밝혀냈다.
이 수는 여러모로 중요하게 쓰여질 수이므로 잘 기억해두는 것이 좋을 것이다.
'교육 > 수알못시리즈' 카테고리의 다른 글
| 함수의 극한 limit of a function (0) | 2020.04.02 |
|---|---|
| 등차수열과 등비수열의 합 Summation of arithmetic progression and geometric sequence (0) | 2020.04.01 |
| 수열의 합과 곱 Summation and product of a sequence (0) | 2020.03.31 |
| 코시 수열 Cauchy sequence (0) | 2020.03.30 |
| 수열의 극한 연산 Operation about limit of a sequence (0) | 2020.03.25 |



