수열이 수렴하는 수열은 많을 것이다.
이들 극한끼리 연산이 가능하다면
수열을 더 자유롭고 깊게 파악할 수 있을 것이다.
일단 수열끼리 계산하기 전에
수렴하는 수열에 특정 상수를 곱한 것도 극한이 있는지 보자.

이런 수열 말이다.
일반항이 a_n 인 수열은 수렴하므로,

수열에 상수를 곱한 수열의 극한은
수열의 극한에 상수를 곱한 것과 같다는 얘기다.
그 다음에 수열 극한 끼리의 사칙연산은 어찌 될지 알아보자.
일단 덧셈으로 시작해보자.

상수 곱과 덧셈의 극한이 성립하므로
수열의 극한도 선형 변환이라고 할 수 있다.
선형 변환이 되니 빼기에 대해서는 음수인 상수를 곱하면 될 일이니,
빼기에 대해서는 덧셈으로 커버칠 수 있다.
덧셈에 대해 했으니, 곱셈에 대해서 하면 될 것이다.
위의 덧셈 식에 있는 극한을 이용해보자.

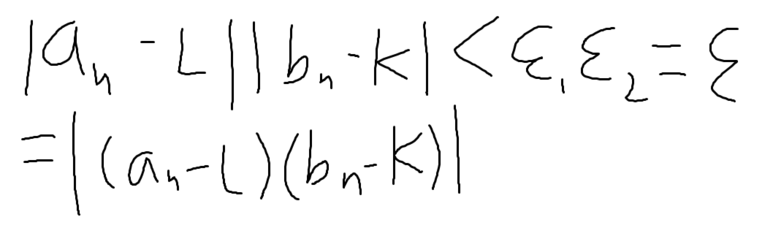

여기에서 식을 분해하여 파악할 수 있을 것이다.
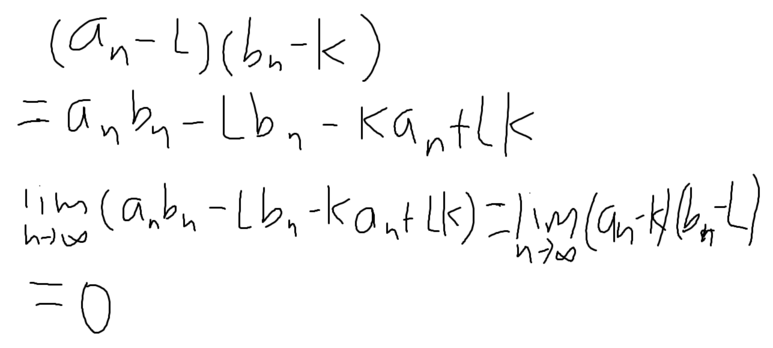
이런 식으로 말이다.
여기서 a_n , b_n은 각각 수렴하고,
상수 수열도 수렴할 것이다.
임의의 상수 c만 반복하는 수열이면, 0보다 큰 임의의 ε 에 대해서
수열의 극한을 c라고 했을 때,
수열의 어느 항이든 c 가 되므로,
l c - c l = 0 < ε
이렇게 되고, 이게 성립하는 자연수 M 이 존재하기 때문이다.
여튼, a_n * b_n 은 수렴 여부가 확실하지 않으므로,
위에 괄호로 묶은 걸 c_n으로 보고 계산을 해보겠다.
일단 c_n은 수렴하기 때문이다.

곱셈에 대해서도 성립함을 알 수 있다.
곱셈의 역 연산이 나눗셈이므로,
수열에 항이나 극한이 0이 아닌 이상은
곱셈이 나눗셈을 커버친다고 보면 된다.
여튼 수열 극한도 사칙 연산에 대해 그대로 성립됨을 알 수 있었다.
'교육 > 수알못시리즈' 카테고리의 다른 글
| 수열의 합과 곱 Summation and product of a sequence (0) | 2020.03.31 |
|---|---|
| 코시 수열 Cauchy sequence (0) | 2020.03.30 |
| 거듭제곱과 로그 Exponentiation and logarithm (0) | 2020.03.24 |
| 수열의 극한 Limit of a sequence (0) | 2020.03.24 |
| 가우스 소거법과 벡터의 차원 Gaussian elimination and dimension of vectors (0) | 2020.03.12 |



