집합 하나가 있을 때,
각 원소에 순서를 매기면 순서가 있는 집합이 되고,
집합의 원소가 수이면, 수열이 된다.

대충 이런 식이다.
이 경우는 집합이 유한한 경우이고,
집합 원소가 수이고 저런 식으로 유한한 집합이 순서가 있을 때는
유한 수열이라고 한다.

수의 무한 집합에 순서를 정하면 무한 수열이 된다.
이런 수열에 패턴이 있으면, 일반항을 구할 수 있고,
몇 번 째 항의 원소가 무엇인지를 파악할 수 있다.
예를 들어 수열이 { 1, 2, ... , n , ... } 이런 식으로 되어있으면,
n 번째 항이 n이 된다는 것을 알 수 있다.
하지만 끝의 항이 뭔지 알 수 없는 수열이다.
그냥 무한히 늘어나는 수열이니까, 무한대(∞) 기호를 써서 발산한다고 표현한다.
반면에, 항은 무한하나 끝의 항이 특정 수가 되는 수열이 있다.
그런 수열은 수렴하는 수열이라고 할 수 있다.
그런데, 이런 걸 말로만 나타내면 실체를 명확하게 파악하기 힘드니
어떻게 형식적으로 나타낼 수 있을지 생각해보자.
어떤 무한 수열의 수렴하는 수가 L 이라고 해보자.
그러면 이런 수열은 굉장히 뒷 순서에 있는 수가 L 과 적은 차이를 보이는 것을 알 수 있다.
수열의 항이 L 과 임의의 오차 범위 이내로 접근한다는 얘기인데,
이런 말로 하면 명확성이 떨어지지 않겠는가?
형식으로 나타내면 다음과 같이 적을 수 있을 것이다.

굉장히 뒷 순서에 있는 수를
자연수에 속하는 M이란 수가 존재하여 M 보다 모든 큰 수 n 이 있으며,
수열의 n번째 항인 a_n 이라 적었고,
그 수가 L 의 차이가 얼마 안 나는 걸
a_n과 L 의 차이가 임의의 0보다 큰 ε 보다 작다고 표현했다.
이런 거를 다른 식으로
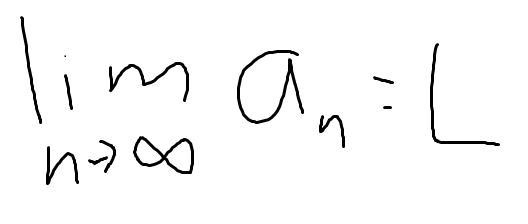
이렇게 표현한다. 항의 순서가 진행될 수록 L에 근접한다는 얘기다.
즉, 수열의 극한이 L 이란 얘기다.

좀 전에 보였던 두 형식이 같은 소리라는 얘기다.
그러면 이렇게 만들어진 형식에서 극한이 유일할 지를 알아보자.
이런 증명에서는 증명하고자 하는 명제의 부정이 옳다는 가정을 하여
모순임을 밝혀 본 명제가 참임을 증명하는 귀류법이란 방법을 써서 증명을 많이 한다.
저 위의 형식에서 극한 값이 서로 다른 수 L과 K 으로 수렴한다고 가정하고,
L < K 이라고 가정해보자.

이렇게 전개할 수 있고,
임의의 0보다 큰 ε에 대해 성립하므로,
빨간색, 파란색 두 값이 같게 ε을 만들면,
ε = ( K - L )/2 > 0
이므로, 위 값에 대해서도 성립한다 할 수 있다.
이 논리에서 봤을 때, 등호, 부등호 관계는

이렇게 되는데, a_n 이 a_n 보다 크다는 사실은 모순이고,
이 결론은 처음에 했던 가정 극한이 유일하지 않다는 것으로부터 도출해낸 결론이므로,
처음했던 가정이 틀렸다는 것을 알 수 있다.
따라서 처음했던 가정의 부정인 본 명제
극한은 유일하다는 사실을 증명해낸 것이라 볼 수 있다.
여기서 크기가 서로 다른 극한을 가진 수열들을 생각해보자.
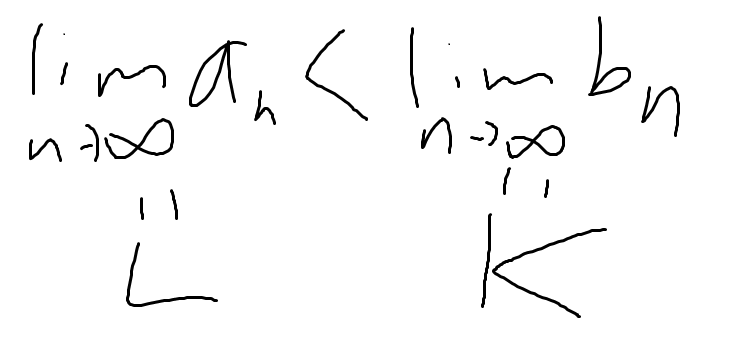
이런 것들 말이다.
만약 이게 성립하면, M이 존재해서
모든 n > M인 n에서 a_n < b_n 가 성립한다고 한다.
이걸 한 번 보여보자.

즉, 바로 앞에 언급한 명제가 맞음을 증명했다.
수렴하는 수열에는 수열의 수가 존재하는 범위가 있을 것이다.
이런 성질을 가진 수열을 유계 수열이라 일컫는데,
이런게 당연하지 않냐고 하지만 조금 명확하게 하기 위해서
형식적으로 따져보도록 하자.

아까봤던 이 형식에서 따지면,
ε = 1 인 M 도 존재함을 알 수 있을 것이다.
1 이 0 보다 크니까 말이다.
굳이 1을 가지고 온 이유는 수열의 범위가 있는지를 파악하는 거기 때문에
범위 파악을 쉽게 할 만한 수를 가져 왔다.
여튼, 전개를 해보자.

여기에서 수열의 절대값의 최대값은
유한집합의 최대값을 구하는 걸로 바꿀 수 있으며,

이렇게 나타낼 수 있을 것이다.
저 형식은 중괄호 안에 있는 것 중에 가장 큰 수라는 뜻이다.
예를 들어 max { 1, 2, 3 } = 3 이런 식이다.
M보다 큰 수 n에 대해서 a_n 의 절대값이 1+l L l 보다 작으니,
괄호 안에 저 것을 넣었다.
그러면, 이 절대값으로 된 집합의 임의의 항은 G보다 작거나 같기 때문에
수열은 -G에서 G 까지 범위 내에 있음을 알 수 있다.
즉, 수렴하는 수열은 존재하는 범위가 있으며, 이는 유계 수열이라는 뜻이 된다.
수열이 있을 때 거기에서 일부를 따로 빼내서 수열을 만든 수열을 부분 수열이라 한다.

예를 들어 B는 A 원소 중 홀수 번째 원소만 빼내서 수열을 만들었으므로,
B는 A의 부분 수열이 된다.
조금 더 일반화해서 표현하면,

이런 식으로 표현할 수 있다.
부분 수열과 본 수열의 극한이 같은 지를 알아보자.
일단 M보다 큰 k가 있을 때, n(k)는 k 보다 크거나 같을 것이다.
자연수 중에서 순서대로 띄엄띄엄 고른 것 중에 k번 째로 고른 수가 k 작을 리 없지 않는가?
임의의 k에 대해, n(k) > = k > M 이므로,
ㅣa_n(k) - L ㅣ< ε
이므로,

이게 성립한다.
'교육 > 수알못시리즈' 카테고리의 다른 글
| 수열의 극한 연산 Operation about limit of a sequence (0) | 2020.03.25 |
|---|---|
| 거듭제곱과 로그 Exponentiation and logarithm (0) | 2020.03.24 |
| 가우스 소거법과 벡터의 차원 Gaussian elimination and dimension of vectors (0) | 2020.03.12 |
| 선형 변환 Linear transformation (0) | 2020.03.06 |
| 일차/선형 독립 Linearly independent (0) | 2020.03.06 |



