벡터들의 조합으로 만들어지는 공간이 있다.
이게 벡터 갯수나 벡터의 성질에 따라 공간의 차원이 달라진다.

예를 들어 영벡터가 아닌 벡터가 3개 있는데,
한 벡터가 다른 벡터의 선형 결합으로 이뤄졌다면,
벡터 a, 벡터 b의 선형 결합으로도 공간을 만들 수 있으므로,
저 벡터가 이루는 공간은 3차원 보다 적다는 걸 알 수 있지 않는가?
저 벡터 c 를 이항시켜면, 벡터 3개의 선형 결합의 합이 영벡터가 될 것이다.
이 때 이런 상황을 일차/선형 종속( linearly dependent )라고 한다.
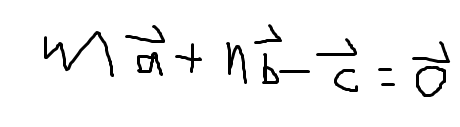
특징을 보면, 벡터 앞의 수가 0이 아닌 수로 벡터의 일차결합을 했는데,
영벡터가 만들 수 있다는 점이다.
다음 경우로 넘어가서

만약에 벡터 3개가 있는데,
어느 벡터도 다른 벡터의 조합으로 나타낼 수 없다면,
벡터가 이루는 공간은 3차원이 될 것이다.
이건 일차/선형 독립(linear independent)가 된다.
저들의 선형 결합으로 영벡터를 만드려면
벡터와 곱하는 숫자가 모두 0이 되어야지 가능할 것이다.
이러한 사실을 일반화 시키면 다음과 같이 얘기할 수 있을 것이다.

a_1 부터 a_n 까지 전부 0 밖에 되지 않는다면, 일차/선형 독립이고,
0이 하나라도 존재하는 조합이 나오면 일차/선형 종속이 된다는 얘기다.
구성 요소 중에 영벡터가 속하면 선형 종속이 된다는 얘기가 되기도 한다.

m차원 벡터 n개 조합한 벡터를 생각해볼 때,
이게 일차/선형 독립인지를 생각해보자.
이 벡터가 영벡터일 때, x_1 ,... , x_n 값이 어떻게 되는지를 봐야할 것이다.
m > = n 이라면, x_1 = ... = x_n = 0 일 때, 일차/선형 독립이 될 것이다.
임의의 벡터가 다른 벡터들의 합으로 만들어지지 않기 때문에,
벡터로 만들어지는 공간의 차원은 벡터의 갯수 만큼의 차원이 된다.
n 차원이 된다는 얘기이다.
미지수 중 하나라도 0이 아니면 일차/선형 종속이 된다.
벡터로 만들 수 있는 공간의 차원이 n 차원 미만의 차원이 된다는 얘기다.
이 부분은 달리 생각할 부분은 없다.
m < n 일 때가 좀 달리 이야기할 부분이 있다.
위 식은 연립방정식으로 바꿀 수 있고,
이를 가우스 소거법으로 근을 구하면, 마지막 부분이

빨간 줄 처럼 나오는데, 우변에 0이 나오는 건
0에서 어떤 수를 곱하고 다른 0에서 어떤 수를 곱하고 더해도 0이기 때문이다.
여튼, x_m , ... , x_n 을 0이 아닌 수로 조합해도 값이 나오므로,
m < n 일 때는 무조건 일차/선형 종속이 된다.
벡터로 만들 수 있는 공간이 n차원 보다 작다는 얘기이다.
어떤 차원의 벡터로 해당 벡터보다 더 높은 차원의 공간을 만드는 건 직관적으로 생각해도 타당하지 않지 않는가?
벡터의 차원 수 보다 벡터의 수가 많으면 이건 일차/선형 종속이고,
일차/선형 독립이 되려면 벡터의 차원 수 보다 벡터의 수가 같거나 적어야 한다.
그래서 이 때 벡터로 만들 수 있는 최대 차원 수는 m차원이 될 것이다.
이상으로 일차/선형 독립과 종속에 대해 알아보았다.
이걸로 벡터로 이룰 수 있는 차원을 얼추 파악할 수 있었고,
가우스 소거법과 함께 쓰면 벡터로 이루는 공간의 차원을 알 수 있다.
'교육 > 수알못시리즈' 카테고리의 다른 글
| 가우스 소거법과 벡터의 차원 Gaussian elimination and dimension of vectors (0) | 2020.03.12 |
|---|---|
| 선형 변환 Linear transformation (0) | 2020.03.06 |
| 연립방정식 근사치 해 구하기 Solving close solution of system of equations (0) | 2020.03.04 |
| 행렬식으로 연립방정식 해 구하기 Getting solution of equation system by determinant (0) | 2020.03.04 |
| 벡터와 행렬, 행렬식과 부피 관계 Relationships between vector and matrix, and between determinant and volume (0) | 2020.03.01 |



