행렬식으로 연립방정식 해 구하기 Getting solution of equation system by determinant

행렬식으로 할 수 있는 것이 여러 가지 있다.

그 중에 하나가 연립방정식의 해를 구하는 일이다.

연립방정식에서 행렬식이 나왔으니,

소거법 이외의 방법인 행렬식으로 구하는 것이 의미있는 작업이라 할 수 있겠다.

​

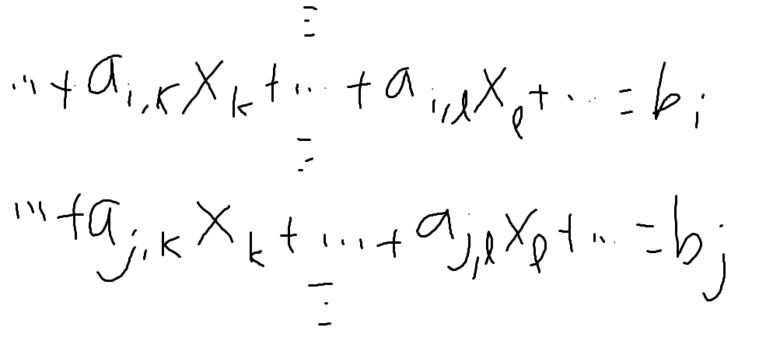
이렇게 연립방정식이 있을 때,

( 1 =< i,j,k,l =< n)

방정식의 근을 다음과 같이 나타낼 수 있다.

​

그럼 왜 그런지 알아보자.

행렬식 특징이

​

det ( ... , A_i , ... A_i, ... ) = 0

​

det ( ... , a A_i + b B_i, ... , A_ j ,... )

= a det ( ... , A_i , ... ,A_ j , ...) + b det ( ... , B_i , ... , A_ j , ... )

​

이렇게 있으므로, 이걸 이용하여 왜 그런지 보이겠다.

분자 부분이 이렇게 나오므로,

결과를 위 분수식에 대입하면 행렬의 행렬식은 약분이 되므로,

남는건 x_k 뿐이다.

그래서 근이 이런 식으로 나온다.

​

x_k 를 구하고 싶으면, k번째 열에 방정식 등호 옆에 적힌 상수를 넣어서

행렬식을 구하고, 방정식을 행렬화한 행렬의 행렬식을 나누면 된다.

물론 방정식의 행렬식이 0이 되면 안되겠다.

​

이렇게만 적으면 감이 잘 안오니

예시를 하나 들면 이해하기 쉬울 것 같다.

이렇게 방정식의 해를 구할 수 있다.

이 방법이 유용할 때가 있으니 알아두면 좋다.