
이런 연립방정식이 있을 때,
m과 n에 따라 근의 양상이 달라진다는 사실을 알 것이다.
m < n 이면, 근이 무수히 많고,
m = n 일 때, 유일한 근이 나올 수 있는 조건이 되고,
m > n 일 때는 특수한 경우를 제외하고는 근이 없다.
마지막 경우, m > n 일 때에 근을 구하지 못한다면,
그 근사치라도 구해보는 것도 나쁘지 않을 것이다.
근사치를 구해보도록하자.
연립방정식은 행렬로 나타낼 수 있으므로 행렬로 나타내보도록 하자.

앞에 것을 A, 뒤에 거를 X 로 나타낼 수 있을 것이고,
이 표현을 AX라고 표현할 수 있을 것이다.
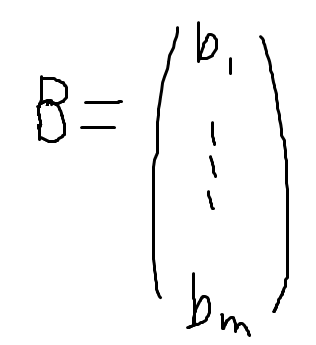
가장 위에 연립방정식 등호 오른쪽 수를 행렬로 나타내면 이런 식으로 나타낼 수 있고,
이를 행렬 B라고 하자.
행렬 X와 행렬 B는 벡터의 형식으로 볼 수도 있다.
X는 n차원 벡터 , B는 m 차원 벡터 이런 식으로 말이다.
AX를 조금 다른 방식으로 표현해보자.
그리고 그 결과를 Y로 표현해보자.
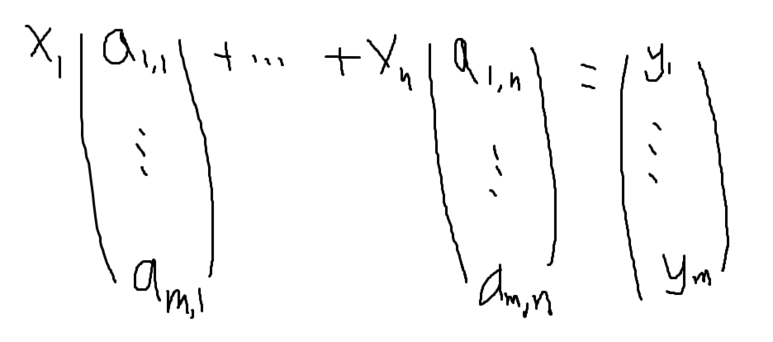
x_1, ... , x_n 이 미지수이므로, Y도 미지수로 이루어진 행렬이다.
행렬 A의 각 열 행렬을 벡터로 생각하면,
Y가 만들어내는 공간은 n개의 m차원 벡터가 만들어낸다고 볼 수 있다.

이 벡터들이 만들어내는 공간은 n차원 이하의 공간이다.
벡터 n 개가 평행한 벡터가 없고, 어느 벡터라도 다른 벡터들의 연산으로 만들어질 수 없다면,
n 차원 공간이 되겠지만,
평행하거나 다른 벡터들의 연산으로 만들 수 있는 벡터가 존재한다면,
n차원보다 작은 차원의 공간이 된다.
m 차원에서 행렬 B가 나타내는 점이 앞에 설명했던 공간에 없다면,
앞에 설명했던 n공간에서 가장 가까운 점이 아까 설명했던 방정식의 근사치 해가 될 것이다.
그러면 그 근사치 해는 B에서 그 공간에 내린 수선의 발이 될 것이다.
해당 공간 밖에 있는 점에서 그 공간까지의 거리를 얘기할 때,
공간에서 점까지 가장 짧은 구간의 길이로 얘기하지 않는가?
이것도 그림으로 그리면 대충 이런 식이다.

B - AX 는 해당하는 벡터는 그림의 공간과 수직하므로,
공간 안에 있는 공간을 만들어내는 A의 열벡터들과도 수직하다고 할 수 있다.
그러면 B - AX 와 A의 열벡터는 그 내적의 값이 0이 되어야 한다.
그러면, 표현은 다음과 같이 할 수 있다.

A 옆에 T 붙은 건 A의 전치행렬이란 뜻이다.
우리가 구하는 목적은 근사한 해이기 때문에 X를 어떻게 표현할 지를 보는 것이므로,
X에 대한 식을 세워야 한다.

식을 세우면 위와 같이 된다.
방정식의 수가 미지수 개수보다 많은 연립방정식에서 근사치를 어떻게 구하는 지를 알아보았다.
이게 점이 여러개 있을 때, 이 점이 이루는 패턴은 무엇인지 파악할 때 많이 쓴다.
이런 방식을 선형 최소제곱법 혹은 제곱대신에 자승을 붙여서 쓰기도 한다.
간단한 예시를 보자.
자료값이
|
x |
x_1 |
... |
x_n |
|
y |
y_1 |
... |
y_n |
이런 식으로 있을 때, 개략적으로
y = ax + b
형태로 표현하고자 한다.
이 때, 구하고자 하는 값은 a, b 의 값이므로,
행렬로 다음과 같이 표현할 수 있다.

구하려는 쌍을 X 행렬에 넣고,
변수는 a와 곱해지도록, 상수는 1을 넣어 b가 살아나도록 할 수 있다.
그러면, y_i = a x_i + b ( 1 =< i =< n )
이렇게 된다.

그러면 a,b는 이 식을 통해서 구할 수 있다.
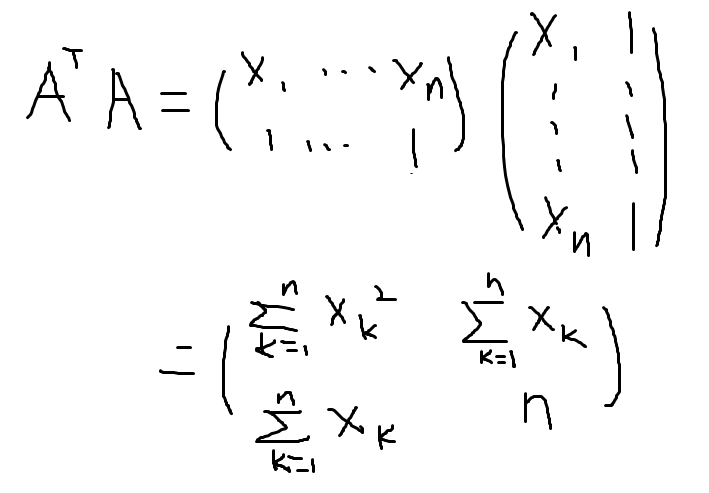


이렇게 a,b 값을 근사할 수 있다.
행렬은 교환법칙이 성립하지 않는 것이지 결합법칙은 성립되기 때문에
위와 같이 계산해도 된다.
여튼 식만보면 상당히 복잡하다.
그래서 이런 계산을 할 때는 컴퓨터의 도움을 받는다.
사실 이것도 썩 좋은 일반화 방법은 아니라,
다른 전문적인 일반화 시키는 방법도 있다고 한다.
이걸로 일반화 하는 방법 쪽에 개념 좀 잡았고,
살짝 맛 봤다 정도만 생각하면 될 것 같다.
'교육 > 수알못시리즈' 카테고리의 다른 글
| 선형 변환 Linear transformation (0) | 2020.03.06 |
|---|---|
| 일차/선형 독립 Linearly independent (0) | 2020.03.06 |
| 행렬식으로 연립방정식 해 구하기 Getting solution of equation system by determinant (0) | 2020.03.04 |
| 벡터와 행렬, 행렬식과 부피 관계 Relationships between vector and matrix, and between determinant and volume (0) | 2020.03.01 |
| 행렬식과 행렬 Determinant and matrix (0) | 2020.02.28 |



