행렬식이란게 행렬이란게 생기기 전에 만들어진 것이라고 한다.
이게 정방행렬의 값을 정하는 식으로 되면서 행렬식이 되는 것 같은데,
determinant 가 애당초 직역하면 결정자의 의미이고 수로 나타내기 때문에,
뭔가를 결정하는 값일 것이다.
행렬은 연립방정식을 표현하는데서 비롯되었으므로,
행렬식 또한 연립방정식과 연관이 있을 것이다.
미지수의 수와 같은 수의 방정식들이 연립되어있는 연립방정식의 해에 대해 얘기하면서
이 값이 나온 것으로 알고 있는데, 아래를 보면서 생각해보자.

이런 연립방정식이 있을 때,

이런 식이 성립한다고 하면,
b_i / b_j 에 따라
이 연립방정식의 공통해가 무수히 많거나 없게 되는 경우가 있다.
여튼 저 식만 성립하게되면
이 연립방정식의 근이 유일하지 않다는 건 똑같다.
이런 성질을 수로 나타내면 연립방정식을 파악하기 편할 것이다.
이런걸 행렬식(determinant)라고 정하고 이를 어떻게 나타낼지 생각해보자.
미지수와 방정식 2개 있는 연립방정식부터 생각해보자.

이런 식이 있다고 할 때,
두 방정식 미지수 항의 비가 같다고 하면,

식을 이런 식으로 전개할 수 있다.
마지막의 있는 표현을 방정식의 결정자, 행렬식이라고하면,
두 방정식 미지수 항의 비가 같으면 행렬식이 0이 되는 것이다.
저 마지막 표현의 값이 0 이 아니라는 것은 저 값이 0이 아니라는 뜻이므로,

이렇게 표현할 수 있다.

행렬식을 잘 살펴보면,
앞의 첨자 숫자와 뒤의 첨자 숫자 관계를 통해서
식을 달리할 수 있는데,
첨자 순서가 1,2 의 순서이므로,
여기서 순서가 바뀐 횟수만큼의 숫자를 형식으로 정하면,
N(1,2) = 0, N(2,1)=1
이 될 것이다.
이를 이용하여 식을 세우면,

이런 식으로 세울 수 있을 것이다.
각 행에 있는 계수 중 하나만 골라서 곱하고
순서 바뀐 만큼 -1 의 제곱수에 넣고 곱한 형식이 됨을 알 수 있다.
이걸 n개의 미지수가 있는 n개의 연립방정식에 일반화시켜보자.
그러기 위해 함수 하나를 정해보도록 하자.
위의 행렬식에서 앞의 첨자가 다르면, 뒤의 첨자가 다르고,
첨자로 적힌 모든 첨자를 골라야 하므로,
함수는 일대일 대응으로 하는 것이 맞을 것이다.
σ : { 1, ... , n } -> {1, ... , n } , 일대일 대응
이 함수를 뒀을 때,
1에서 n 까지 배열을 바꿨을 때 바꾼 횟수를
N( σ(1), ... , σ(n) )
으로 나타낼 수 있다.
그리고 집합을 하나 만들어보자.

이렇게 집합을 만들고,
(-1) ^ N( σ(1), ... , σ(n) ) = sgn ( σ )
로 만들면, 행렬식을 일반화 할 수 있을 것이다.
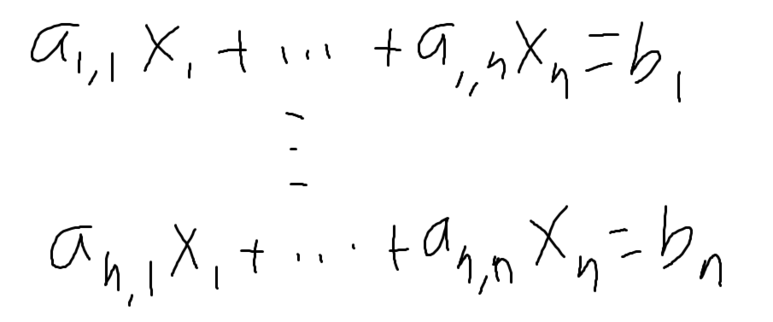
이 식의 행렬식, 결정자는
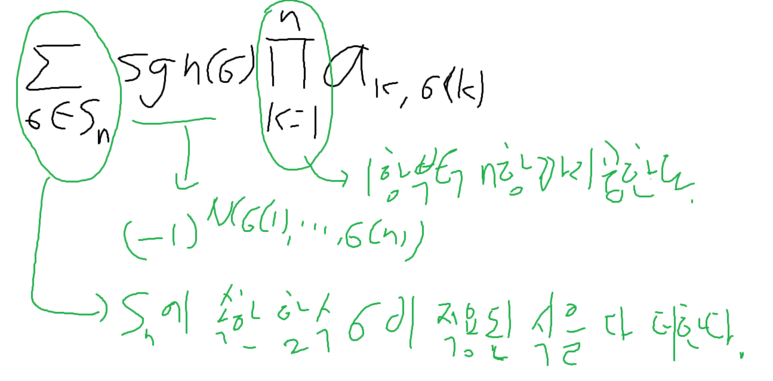
이런 식으로 표현할 수 있다.
그렇다면, 이 식이 행렬식, 결정자로 타당한지 알아보도록하자.
그러려면 행렬식의 여러가지 성질을 파악해야 할 것이므로,
2개 미지수, 식이 있는 연립방정식으로부터 성질을 이끌어내보도록 하자.
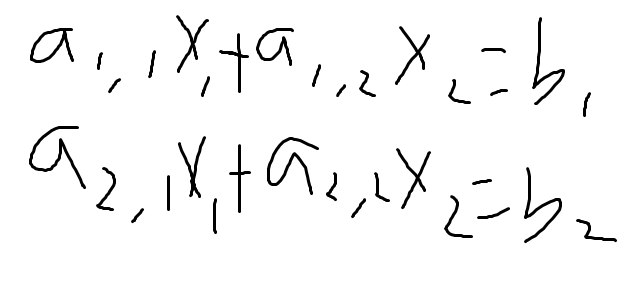
이 연립방정식의 위 아래가 바뀐다면
행렬식의 형태가 바뀌게되는데,

그렇게 되면 이렇게 행렬식의 부호가 바뀌게 될 것이다.
방정식 하나에 다른 방정식을 더하게 되면,

이 방정식의 행렬식, 결정자가 더해지게 된다.
방정식 하나에 상수를 곱한다면


행렬식의 상수배가 되게 된다.
이 성질을 조금 더 간단하게 정리해보자.

이렇게 될 것이고,

행렬식의 기본 단위를 만들면 이와 같은 표현을 할 수 있다.
이걸 n개의 미지수를 가진 n개의 연린방정식에 적용하면,

이렇게 적용할 수 있을 것이다.
여기에 행렬식 기본 단위를 적용해서 파악해보자.

행렬식은 아래와 같은 성질이 있으므로,

σ : { 1, ... , n } -> {1, ... , n } , 일대일 대응
이 함수를 적용하고,

이 집합을 만들어서 행렬식에 적용시킬 수 있을 것이다.
(-1) ^ N( σ(1), ... , σ(n) ) = sgn ( σ )
아까 적용했던 이 식 까지 넣으면,

마지막 줄의 값은 sgn( σ ) 이다.
그래서 식을 전개하면

행렬식의 성질로 유도한 값과
2개 미지수와 식이 있는 연립방정식 행렬식에서 추출한 특징으로
일반화한 값이 같으므로,
이 식을 행렬식으로 정의하는 것이 타당하다.
'교육 > 수알못시리즈' 카테고리의 다른 글
| 벡터와 행렬, 행렬식과 부피 관계 Relationships between vector and matrix, and between determinant and volume (0) | 2020.03.01 |
|---|---|
| 행렬식과 행렬 Determinant and matrix (0) | 2020.02.28 |
| 벡터의 연산 법칙 Operation rules in vector (0) | 2020.02.22 |
| 좌표 공간과 벡터 Coordinate space and vector (0) | 2020.02.21 |
| 벡터와 그 연산 Vector and its operation (0) | 2020.02.21 |



