저번 포스트에 행렬식에 대해서 얘기 했었다.
행렬식과 행렬이 연립방정식에서 나온지라
연립방정식에서 나온 결정자가 행렬식으로 번역되는 일이 발생한 것이 아닌가한다.
연립방정식에서 계수만 빼서 수를 나열해놓게 행렬이니 당연한 결과일 것이다.
그래도 행렬로 행렬식을 파악하면,
연립방정식에서 파악하는 것보다 조금 더 간단하고 다양하게 파악할 수 있는 부분이 있다.
순서는
1. 행렬식으로 행렬의 성질 증명
(이건 이전 포스트 내용과 비슷하여 넘어가도 관계없지만 관심있으면 읽어봐도 된다.)
2. 곱행렬의 행렬식
3. 행렬식으로 역행렬 나타내기
이렇게 전개하도록 하겠다.
1. 행렬식으로 행렬의 성질 증명
연립방정식과 행렬, 행렬식을 한 번 상기해보자.

위 그림과 같이 관계를 연결지을 수 있을 것이다.
가장 아랫줄의 기호가 좀 익숙치 않을 것인데,
이것도 보면,

이런 뜻을 가지고 있다.
더 자세히 알고 싶으면,
행렬식 Determinant에 들어가서 보면 된다.
행렬식의 특징은

A의 행렬식을 이렇게 정할 때,

이런 성질을 가지는데,
링크에 있는 포스트에서 유도했던 방식을 참고하면 된다.
그냥 같다고 봐도 된다.
사실 행렬식 자체로도 증명이 가능하다.
일단, 처음꺼 부터 해보자.

행의 순서를 바꾼 것을 적용하기 위해
sgn( τ ) 를 정해뒀다.
그렇게 계속전개하면,
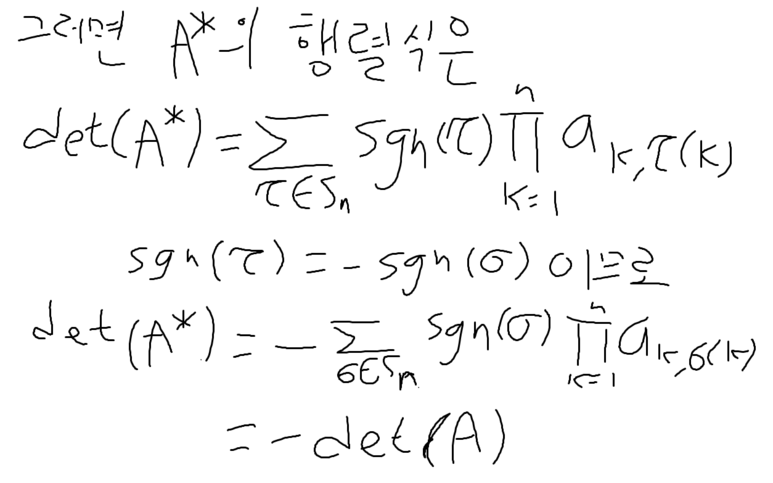
처음 것이 증명된다.
두 번째, 세 번째 것도 계속 증명해보겠다.

이 때, n>=2 여야 행렬식에 대해 말하는 게 의미가 있으므로,
고려하는 범위에서 n!은 짝수가 된다.
그러면,

이 식의 항의 수가 n! 개 이고, 짝수이니

이와 같은 짝을 다 지을 수 있으므로,
행렬식의 값은 0이 됨을 알 수 있다.
두 번째 성질을 보였으니, 마지막 성질을 보도록 하자.

다시금 행렬식으로 정의한 것이

앞에 설명한 세 가지가 적용된다는 걸 알 수 있었다.
2. 곱행렬의 행렬식

AB = C 로 표현했을 때,
C 행렬은 위와 같이 표현할 수 있다.
그러면 C의 행렬식은 다음과 같이 나타낼 수 있다.

여기에서 행렬식의 성질을 이용하여 식을 전개할 수 있는데,
가로 기준이나 세로 기준이나 행렬식 성질이 같고 값도 같기 때문에 관계가 없으므로
이대로 계속 진행하도록 하겠다.

C의 행렬값은 이렇게 나타낼 수 있다.
뒤에 있는 det ( A_1 ... A_n ) = det(A) 이고,
그 앞의 것은 det(B) 와 같다.
행렬을 가로 순서로 고르든 세로 순서로 고르든 같기 때문이다.
결국 det (C) = det(B) det(A) 가 되고,
행렬이 아닌 수는 곱셈의 교환법칙이 성립하고,
C = AB 이므로,
det( AB ) = det(A) det(B)
가 성립함을 알 수 있다.
3. 행렬식으로 역행렬 나타내기
우선, 역행렬이 존재하는 조건부터 알아보자.
AX = I 이면
A와 X가 역행렬이 되는데,
행렬식으로 파악했을 때,
det(A) det(X) = det(I)
이렇게 된다.
행렬식으로부터 det(I) = 1 이란 값을 얻을 수 있으므로,
det(A) 와 det (X) 는 역수가 된다.
수를 0으로 나눌 수 없으므로,
임의의 행렬 A의 행렬값이 0이면,
A의 역행렬은 존재하지 않게된다.
역행렬이 존재하는 조건은 행렬값이 0이 아니어야 한다.
역행렬이 존재하는 조건을 알았으니
역행렬을 표현하는 형식을 생각해보자.
여기에 대한 접근법은 행렬식으로부터 나온다.
행렬식을 다시 상기해보자.

이 모양이다.
이 식을 조금 바꿔서

이렇게 만들고,
σ ( i ) = j 라고 하겠다.
그러면 행렬 A가 있을 때, 행렬식은

앞으로 뺄 것을 i 행으로 하든 j열로 하든 일단 한 줄을 앞으로 뺄 숫자로 지정하여,
( 1=< i,j =< n)
i행에 해당하는 원소와 j열에 해당하는 원소를 제외한 행렬의 행렬값을 만들고,
그것과 빨간색 동그라미 안의 숫자를 곱하는 식으로 A의 행렬값을 표현할 수 있을 것이다.
대신에 A 에 대한 행렬값을 구하는 것이므로,
앞으로 빼고, 그만큼 나머지를 옮긴 수만큼 계산해줘야 한다.

옮긴 횟수는 이 그림을 참고하면 되겠다.
그리고나서 i행에 해당하는 원소와 j열에 해당하는 원소를 제외한 행렬의 행렬값을 만들 것인데,
그러기 위해 새로운 함수 τ 를 만들도록 하겠다.
τ : (1, ... , n-1 ) -> {1, ... , n-1 }, 일대일 대응
이렇게 만들었으면,
i행에 해당하는 원소와 j열에 해당하는 원소를 제외한 행렬식을 세울 것인데,
식은 다음과 같이 세울 수 있다.

i행에 해당하는 원소와 j열에 해당하는 원소를 제외한 행렬에 대한 순서만 고려했으므로
이런식이 나오게 된다.
이 식의 값을 M_i,j 라고 하자.
그리고 det ( A)를 계산하면,
전체적으로 i+j 번 이동했으므로, (-1)^(i+j)를 곱해줘야 한다.
그래서 값을 식으로 세우면,

이와 같이 결과가 나온다.
여기서 조금 더 간단하게 식을 만들면,
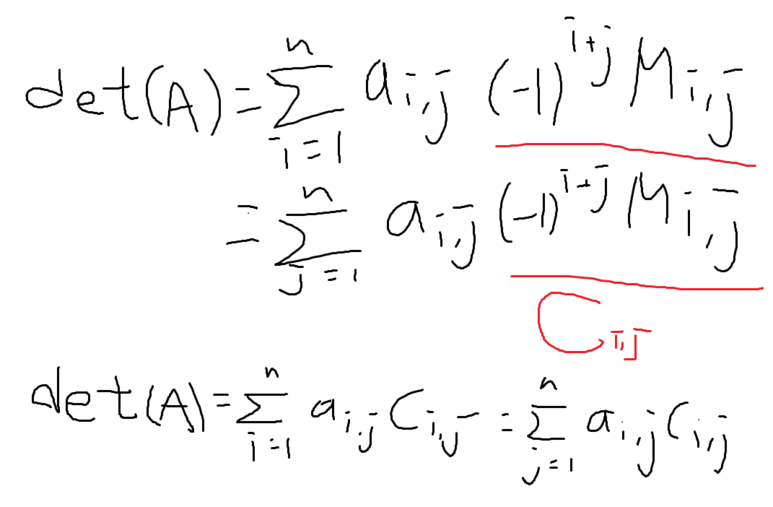
이렇게도 표현할 수 있다.
여기에서 착안해 행렬의 곱을 만들어보자.

만약에 i = j 이면, 그 값은 det ( A) 이다.

만약에 서로 다르다면,

이 값은 0이 된다.
결국 A adj(A) 를 전개하면,
행, 열의 숫자가 같으면, det(A), 다르면 0 이므로,
A adj(A) = det(A) I
가 되고,
A의 역행렬은 adj(A) / det(A) 가 된다.
이렇게 세 가지로 행렬과 행렬식에 대해 알아봤다.
'교육 > 수알못시리즈' 카테고리의 다른 글
| 행렬식으로 연립방정식 해 구하기 Getting solution of equation system by determinant (0) | 2020.03.04 |
|---|---|
| 벡터와 행렬, 행렬식과 부피 관계 Relationships between vector and matrix, and between determinant and volume (0) | 2020.03.01 |
| 행렬식 Determinant (0) | 2020.02.27 |
| 벡터의 연산 법칙 Operation rules in vector (0) | 2020.02.22 |
| 좌표 공간과 벡터 Coordinate space and vector (0) | 2020.02.21 |



