도형을 좌표 공간에 표현할 수 있으므로
벡터 또한 좌표 공간에 표현할 수 있을 것이다.
좌표 각 축과 평행하고 크기가 1인 단위벡터를 정의해서
원점 O에서 임의의 점 P 까지 그은 벡터를 생각해보면,

이런 식으로 표현이 가능할 것이다.
V(e_i) 은 x_i ( 1=< i =< n ) 축과 평행하다는 뜻이다.
p_i * V(e_i) 이란 뜻은 단위벡터 V(e_i)의 크기가 p_i 배이고, 방향은 같은 벡터라는 뜻이다.
벡터 뎃셈 뺄셈의 결과에서 각 단위 벡터를 살려서 나타내고 싶다면,
단위 벡터가 같은 것들 끼리만 연산하게끔 규칙을 정하면 될 것이다.

이런 식으로 말이다.
단위 벡터를 생략하고자 한다면,
좌표 공간 표현하는 것 같이
( p_1 , ... , p_n ) + ( q_1 , ... , q_n ) = ( p_1 + q_1 , ... , p_n + q_n )
이런식으로 적을 수 있을 것이다.
뺄셈은 덧셈의 역연산이므로 덧셈에 대해 정의가 되었으니
좌표 공간 내에서 벡터의 덧셈 뺄셈은 여기까지 얘기하면 될 것이다.
이제 벡터의 내적에 대해 생각해보자.
여기에 대한 접근은 삼각형을 그려 제 2 코사인 정리로 파악하면 될 것이다.

이런 식으로 말이다.
마지막 식은
V(a) = ( a_1 , ... , a_n )
V(b) = ( b_1 , ... , b_n )
이므로

식의 전개는 이런 식으로 된다.
좌표 공간 내에서의 벡터 내적에 대한 것도 정해졌다.
이제 벡터 외적만 정하면 되겠다.
벡터 외적은 3차원에서만 적용되므로 3차원 공간에서 생각하면 될 것이다.
규칙은 아래와 같이 정할 수 있다.

회전은 반시계 방향으로 회전한다는 얘기이다.
다른 조합도 아래와 같이 정할 수 있다.

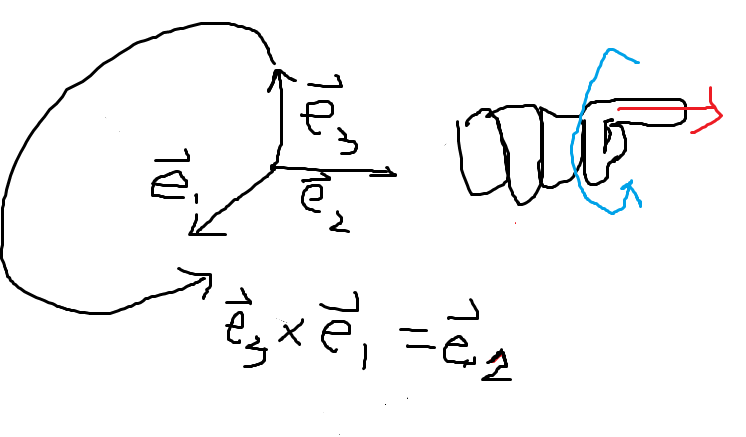
이런 식으로 정할 수 있을 것이다.
순서를 바꾸면 결과에 ' - ' 를 붙이면 될 것이다.
같은 종류의 단위 벡터를 외적하면 회전이 없으므로 0 이다.
벡터 외적 연산을 해보자.
( a_1 , a_2 , a_3 ) x ( b_1, b_2, b_3 )
첫 번째 칸은 두 번째 세 번째 칸의 것들을 계산해서 나온 값이므로,
a_2 * b_3 - a_3 * b_2
이게 들어가게 된다.
같은 식으로 계산 하면,
( a_1 , a_2 , a_3 ) x ( b_1, b_2, b_3 )
=( a_2 * b_3 - a_3 * b_2 , a_3 * b_1 - a_1 * b_3 , a_1 * b_2 - a_2 * b_1 )
이런 식이 된다.
벡터 외적에 대한 계산도 이렇게 정해졌다.
내적이나 외적이나 식을 늘여쓰지 않고 조금 짧게 쓰려면
몇 개 기호를 정해두고 쓰면 될 것이다.
이러면 벡터의 내적을 정할 수 있다.

앞의 기호는 합한다는 기호이다.
덧셈 기호를 여러 번 쓰기 귀찮으니까, 1항부터 n항까지 합친다는 기호를 쓴 것이다.
벡터의 외적도 한 번 정해보자.

식을 이런 식으로 세울 때,
i, j, k 세 기호 중 두 기호만 같아도 값이 0 이므로,
셋 다 다를 때만 추출하면, 6개의 항만 남을 것이다.

벡터의 외적도 간단히 나타낼 수 있다.
좌표 공간 내에서 벡터의 덧셈, 내적, 외적을 나타내보았다.
'교육 > 수알못시리즈' 카테고리의 다른 글
| 행렬식 Determinant (0) | 2020.02.27 |
|---|---|
| 벡터의 연산 법칙 Operation rules in vector (0) | 2020.02.22 |
| 벡터와 그 연산 Vector and its operation (0) | 2020.02.21 |
| 삼각형에서의 사인, 코사인 정리 Theorem about sine and cosine in triangle (0) | 2020.02.17 |
| 피타고라스 삼조 Pythagorean triple (0) | 2020.02.17 |



