이전에 수열의 극한에 대해서 다뤘었다.
수열도 자연수가 정의역인 함수의 일종으로 볼 수 있을 것이다.
f : N -> R
이런 식 말이다.
공역은 실수 집합 R 대신에 다른 집합도 넣을 수 있다.
수열이 수렴할 때 수열의 항 값이 수렴 값 근방으로 가지 않았는가?
이 생각을 함수에 대해서 한다고 하면,
정의역에서 수렴하는 값을 정할 수 있고,
수렴하는 값으로 다가갈 때,
함수 값도 어떤 수렴하는 값으로 다가가게 만들 수 있을 것이다.
그렇다면 함수의 극한을 만들 수 있을 것이다.
이 개념이 나중에 함수의 연속 등 여러가지 개념과 연동해서 쓰일 것인데,
이게 수렴 값보다 작은 값에서 다가갈 때와 큰 값에서 다가갈 때의 일치여부로 판별하므로,
정의는 개구간에서 한다.
예를 들면 x에 대해서, a < x < b 이런 구간 말이다.
상한은 b, 하한은 a 로써 존재하지만,
최대값, 최소값은 없다.
즉, 해당 구간의 임의의 원소가 있을 때, 항상 그 보다 작은 값, 큰 값을 정할 수 있다는 얘기이고,
나중에 다룰 함수의 연속 등의 개념에 써먹을 수 있다는 얘기가 되겠다.
앞에서 서술한 사항을 기호로 쓰면,

이런 형식으로 나타낼 수 있다.
수열의 극한에 자연수에 속하는 모든 n에 대해서 n > M 인 M이 존재한다고 나와있는 부분이
x 와 a 와의 거리가 0초과 δ 미만인 δ 가 존재한다고 서술되었다.
이 때문인진 몰라도 a 로 수렴하는 수열을 만들어서 이 수열이 수렴할 때,
수열 항에 대한 함수가 있어 이 함수의 수열도 수렴한다는 식으로 수열의 극한을 정의하기도 한다.
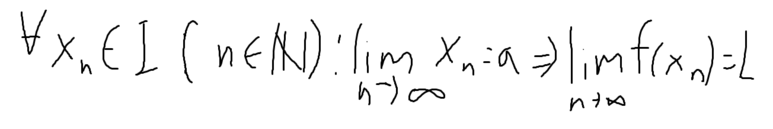
이런 식으로 말이다.
위에 적어놓은 정의에서 그리스 문자 두 개 δ , ε 이 있는데,
각각 distance의 첫 글자와 error 의 첫 글자의 해당하는 그리스 문자라고 한다.
좀 전에 언급했던 좌극한, 우극한이란 놈은
위 정의에 있는 절대값을

이렇게 해놓고, 왼쪽에 있는 걸 정의에 넣으면 좌극한이 되고
오른쪽에 있는 걸 정의에 넣으면 우극한이 된다.
왼쪽에 있는건 a > x 이고, 오른쪽에 있는 건 x > a 이므로,
좌표 평면 상에서 생각했을 때, 각각 a의 왼쪽 , 오른쪽에서 다가오는 형태이기 때문이다.

좌극한, 우극한은 위와 같이 표기한다.
이건 첨자 식으로 표현했지만, 각각 a-0, a+0 으로 표기하기도 한다.
지금 상황은 좌극한, 우극한이 L로 같은 상황이므로,

이런 말이 성립된다.
좌극한 우극한이 같을 때는 함수의 극한은 유일하다.
함수라는게 정의역 원소에서 함수 값이 유일하도록 정의를 했기 때문이다.
두 함수의 극한이 다를 때, 그 근방에서의 크기는 극한에서의 크기 관계와 같은지 보자.

따라서 f(x) 극한과 g(x) 극한 크기 관계는 그 근방에서의 관계에서도 유지됨을 보였다.
함수의 극한도 수열의 극한과 성질이 같음을 알 수 있다.
그러므로 함수의 극한도 사칙 연산에 대해서 성립한다고 할 수 있다.
x와 a간의 거리가 0 초과 δ 미만인 δ 의 존재 부분을 모든 n > M 인 M의 존재로 바꿔 대입하면 된다.
함수의 극한에서 계속 나왔던 0 초과 부분에 대해서 부가적으로 설명하자면,
수열에서 n이 무한대로 간다는 거는 n이 계속 늘고있는 상태를 표현한 것과 같은 맥락으로,
함수의 극한 정의에서 0 초과라 적은 것도 x가 a에 계속 가까이 다가가는 상태를 표현한 것이라 본다.
상수함수

덧셈

상수곱

곱셈

뺄셈과 나눗셈은 덧셈과 곱셈의 역연산이니
상수를 음수로 보고 식을 바꾸고 이항시키면 되니까
덧셈과 곱셈으로 충분하다.
단, 나눗셈은 나누는 함수의 값이 범위 내에서 0이 되면 안된다.
'교육 > 수알못시리즈' 카테고리의 다른 글
| 리만 적분 Riemann integral (0) | 2020.04.05 |
|---|---|
| 함수의 연속 Continuity of a function (0) | 2020.04.02 |
| 등차수열과 등비수열의 합 Summation of arithmetic progression and geometric sequence (0) | 2020.04.01 |
| 상수 e The constant e (0) | 2020.03.31 |
| 수열의 합과 곱 Summation and product of a sequence (0) | 2020.03.31 |



