이전에 단일 변수에 대한 리만 적분에 대해서 알아보았다.
범위를 잘게 쪼개 놔서 쪼개놓은 범위에서 최소값 기준의 합과 최대값 기준의 합이 서로 수렴될 때
이런 거를 리만 적분이라고 했다.
이번엔 다변수에 대한 리만 적분에 대해 생각해볼 건데,
최소값 기준 것을 하합 또는 리만 하합.
최대값 기준 것을 상합 또는 리만 상합이라 서술하면서 글을 전개하도록 하겠다.
범위 I, J에 대해 리만 적분 가능한 함수 f : X x Y -> R 이 있다고 하고,
I ⊆ X, J ⊆ Y 라고 하자.
여기서 I 를 m 개로 나누고 J를 n 개로 나누어 함수가 나타내는 영역의 크기를 근사할 수 있을 것이다.
이 때 범위 I x J = A 라고 하면, A는 mn 개의 범위가 될 것이다.
여기서 리만 적분 값은 다음과 같이 나타낼 수 있을 것이다.

적분 기호 옆에 적은 거는 적분할 영역을 아래에다 적은 것이다.
범위가 어디에서 어디까지다 라고 적는 방법도 있고,
이 범위에서 적분할 것이다 라고 적는 방법도 있으니
이런 방법도 참고해두면 좋겠다.
여튼 , 이 세 가지가 과연 같은 값이 될 지 알아보자.
일단 리만 하합에 대해서 정의하면 다음과 같다.

상합은 위 기호에 L 대신에 U를 붙혀 나타낼 수 있다.
A의 일부 영역 A_k,l 에서 다음과 같은 관계를 나타내므로,


리만 하합과 상합의 관계로 나타내면,

이런 식으로 될 것이고,
f( x, y ) 는 정의된 영역에서 리만 적분이 된다고 했으니,
위에 적은 값들은 다 하나의 값으로 수렴이 되고,
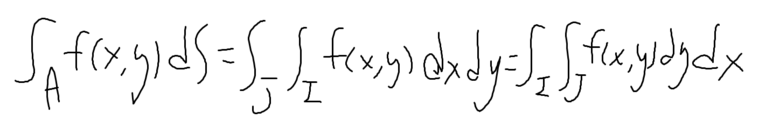
세 가지 표현은 결국 같은 값이 된다.
여기서 리만 적분 가능한 함수 f ( x, y, z ) 가 있을 때도 같은 방식으로 적용할 수 있다.

함수 f는 V 영역 내에서 리만적분 가능하므로,
V 영역 일부인 I, J, K 에서 어느 순서로 적분해도 같은 값이 나온다.
여기서 확장하면, 리만 적분 가능한 함수 f를 다음과 같이 정했을 때,

이런 식으로 쓸 수 있고,
적분 순서를 바꿔도 값은 같게 된다.
적분을 여러번 하는 걸 중적분이라고 하는데,
이 정리로 영역 내에서 리만 적분 가능한 함수에 대해
중적분할 때 각 변수에 대해 적분을 하는 방법으로 할 수 있는 근거가 마련되었다고 보면 된다.
'교육 > 수알못시리즈' 카테고리의 다른 글
| 평균값 정리 Mean value theorem (0) | 2020.04.13 |
|---|---|
| 도함수/미분 Derivative (0) | 2020.04.13 |
| 리만 적분 Riemann integral (0) | 2020.04.05 |
| 함수의 연속 Continuity of a function (0) | 2020.04.02 |
| 함수의 극한 limit of a function (0) | 2020.04.02 |



