이 적분도 리만적분에 기반한 건데,
이전에 했던 적분은 범위가 정해져있는 적분이라고 한다면,
이번에 다룰 것은 범위가 변동되는 적분이다.
표현하자면 다음과 같다.

우선 정적분에 대해서 생각해보면,

이런 거를 아래와 같이 표현할 수 있을 것인데,

0과 1부터 n까지 양의 정수 i, j에 대해,
i < j 일 때, x_i < x_J 라고 하면, 저 절대치는 그냥 그대로 양수가 되고,
min 들어간 거와 max 들어간 거는 서로 수렴해서 같은 값이고,
이 식에서 가장 끝 항이 x_n 이 될 것인데,
이 값은 n이 얼마이건 간에 b가 될 것이므로,
이 식에는 b가 들어간다는 사실을 알 수 있다.
그리고, 첫 항인 x_0 = a 도 무조건 들어갈 것이므로,
해당 식은 a와 b가 들어간 식으로 볼 수 있다.
이제 이 형식으로 넘어와서,

이 식은 범위의 끝인 x와 a가 식에 있으므로,
Φ ( x, a ) 라는 방정식을 세울 수 있다.
미지수로 둘 건 x 이고 a는 상수로 둘 것이기 때문에,
이 식을 x에 관한 방정식으로 표현할 것이다.
그러면 방정식은 미지수 부분과 상수 부분으로 나눌 수 있을 것이다.
미지수 부분은 F ( x ) 로 두고, 상수 부분을 C로 두면,
Φ ( x, a ) = F ( x ) + C
로 만들 수 있고,
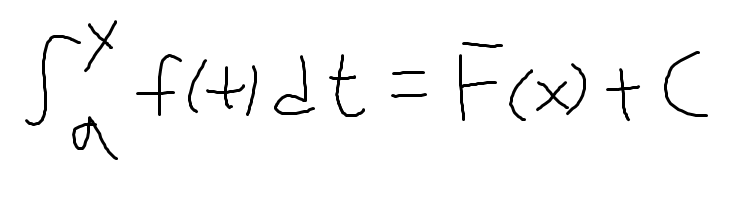
이렇게 표현할 수 있다.
t를 x로 바꿔서 표현하고 싶을 때는
x 범위가 정해지지 않아서 인테그랄 표시에 범위를 적지 않고,
다음과 같이 표현할 수 있다.

이렇게 말이다.
부정적분에서 나온 표현으로 정적분을 다른 방식으로 표현할 수 있을 것인데,
정적분에서의 다음과 같은 성질을 보고 표현법을 파악하도록 하자.

이 성질로부터,

정적분에 대한 또 다른 표현이 이런 식으로 나왔다.
t 대신에 x를 넣어도 된다.
여기서 F (x) 와 f(x) 와의 관계가 궁금할 것인데,
이 관계에 대해서는 다음에 얘기하도록 하겠다.
'교육 > 수알못시리즈' 카테고리의 다른 글
| 테일러 급수 Taylor series (0) | 2020.04.16 |
|---|---|
| 미분과 적분과의 관계 Relation between differential and integral (0) | 2020.04.13 |
| 함수 덧셈에 관한 리만 적분 Riemann integral about addition of functions (0) | 2020.04.13 |
| 평균값 정리 Mean value theorem (0) | 2020.04.13 |
| 도함수/미분 Derivative (0) | 2020.04.13 |



