이전 포스트에서 방정식에 대해 대충 훑어보면서
연립방정식을 보았다.

이런 식 말이다.
이렇게 쓰게되면,
각 식에 있는 미지수를 식 적을 때 마다 일일히 적어야하는 불편함이 있다.
역사적으로도 이걸 해소하기 위한 방법이
계수는 계수대로 따로 적고 미지수는 미지수대로 따록 적는 방법이었다.
일단, 이 방정식을 조금 더 편하게 적는 방법은

이런 식일 것이다.
적어도 같은 미지수를 여러번 적는 일은 없지 않는가?
여기서 조금 더 깔끔하게 표기하는 방법이
계수와 미지수를 분리하는 방법일 것이다.
방법은 두 가지 정도가 있을 것인데, 살펴보자.

그런데, 이런 식으로 적으면 공백이 생기지 않겠는가?
실제로 무슨 목적으로 지금의 형식이 되었는지는 모르겠으나,
공백을 적게 하기위한 목적도 있었는지,
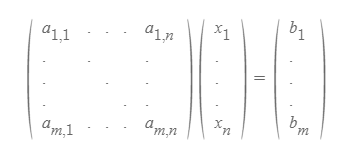
이런 식으로 적도록 정해놓았다.

이런 연립 방정식을
↓

이렇게 되고, 조금 더 진화해서

계수 미지수 따로 분리해서 깔끔하게 적어놓은 형태가 되었다.
저 괄호와 숫자들의 묶음을 행렬(matrix)라고 한다.
이렇게 적으면, 계수는 같고 미지수가 다른 연립 방정식을 여러개를 표현할 수 있다.
연립 방정식을 더 효율적으로 표현할 수 있다는 얘기다.
개수가 많을수록 더 효율적이다.

이렇게 표현하는게

.
.
.

이렇게 일일히 표현하는 것 보다 효율적이지 않는가?

이 때, a에 첨자 붙인 것들로 이루어진 행렬을 A라고하고,
x에 첨자 붙인 것들로 이루어진 행렬을 X,
b에 첨자 붙인 것들로 이루어진 행렬을 B라고 할 때,
AX = B 로 표현할 수 있을 것이고,
이것을 행렬의 곱으로 정의할 수 있을 것이다.
이런 식으로 정의할 때 행렬의 곱은 숫자의 곱과 다르게 교환법칙이 성립되지 않는다.
왜 성립이 되지 않는지를 보도록하자.

행렬의 곱이 되려면 왼쪽 행렬의 열의 수와 오른쪽 행렬의 행의 수가 같아야 한다.
그렇지 않으면 두 행렬은 아얘 교환해서 연산이 되지 않는다.
연립 방정식에서 파생된 게 행렬의 곱이니
왼쪽 부분을 계수들만 모아놓은 것
오른 쪽 거를 연립 방정식의 미지수를 모아놓은 것의 컨셉을 잡아서 연산을 생각하면,
조금 전에 했던 말의 의미를 수월하게 이해할 수 있을 것이다.
만약에 m=p라고 해도,
AX의 결과는 m행 p열, 즉 m행 m열 행렬인데,
XA의 결과는 n행 n열 행렬이다.
n=m이 아닌 이상 결과로 나오는 행렬의 행, 열의 수가 달라진다.
또한 n=m 일지라도,
행렬에 있는 숫자가 같을진 장담할 수 없다.
AX = B, XA = C 라고 하자.

두 행렬의 행과 열이 같다고 해도 행렬의 곱의 교환법칙이 성립하지 않음을 보였다.
즉, 일반적인 경우에는 두 행렬의 곱이 성립하지 않는다고 봐야한다.
앞으로 행렬 곱을 계산할 때는 순서를 반드시 지켜야한다는 얘기다.
그러면, (AB)C 와 A(BC)는 어떨까?
둘의 순서는 같은데 괄호가 다르다. 결과가 같을까?
AB = P 라고 하고, BC =Q 라고 놓아보자.
P, Q의 임의의 원소는 다음과 같이 전개할 수 있다.

(AB)C = PC = V
A(BC) = AQ = W
라고 하자.
그럴 때, V와 W의 임의의 원소를 전개해보자.


V의 임의의 원소와 W의 임의의 원소가
v_i,j = w_i,j
서로 같으므로, V=W 이고,
(AB)C = A(BC) 이므로,
곱셈에 대한 결합법칙은 성립한다.
괄호를 어떻게 쳐서 곱하든 상관없다는 뜻이다.
곱하는 순서는 지켜야하지만, 묶는 거는 순서만 지키면 된다는 얘기다.
행렬의 곱셈을 정했는데, 덧셈은 어떻게 정할 수 있을까?
연립 방정식으로 돌아와서,
미지수가 같고 계수가 다른 연립 방정식을 더해보자.

이런 두 개 연립 방정식을 더하는 거 말이다.
그러면 형태는 아래와 같이 될 것이다.


이게

이런 식으로 표현 되고, 이 연립방정식 시스템은 AX=B 로 표현한다고 하자.

이게

이런 식으로 표현 되니, CX=D 가 된다고 하자.
AX와 CX를 더하면,

이런 식으로 표현할 수 있으며,
아래와 같이도 표현할 수 있다.

이건 또,

이렇게 표현할 수 있고, 연립 방정식을 보면,
AX + CX = B+D 임을 알 수 있다.
행렬 형식을 GX = H로 볼 때,
AX + CX = GX
B+D = H 이다.
B+D = H 를 보면
행렬의 행, 열의 수가 같아야 행렬의 덧셈 연산이 가능하며,
그 행렬 원소의 덧셈은 행이 모두 똑같은 것 끼리 더해져야 한다.
그리고 행렬 분해 작업을 해서 전개하면,

여기서

이렇게 되고, 같은 미지수 별로 묶으면,

이렇게 될 것이고, 같은 행 끼리 덧셈이 가능하므로

이렇게 표현할 수 있다. 이 형태를 행렬 곱으로 나타내면,
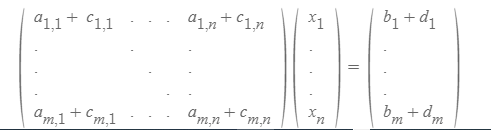
이렇게 된다. 이런 연산이 원활하게 되려면,
행렬 덧셈에서 행렬 원소의 행 뿐만 아니라 열까지도 같아야 덧셈이 가능하게 하는 것이 타당할 것이다.
그러면 AX+CX=GX 가 (A+C)X = GX 로 행렬 곱셈 분배법칙도 성립하게 된다.
행렬에 있는 원소끼리 더해서 나오는 게 행렬의 덧셈이므로
a_i,j + c_i,j = c_i,j + a_i,j (1=< i,j =<n)
임의의 원소 덧셈이 성립하므로, 행렬의 덧셈은 교환법칙이 성립된다.
A+C = C+A = G
이런 논리로 결합법칙도 성립합을 알 수 있다.
(A+B)+C = A+(B+C)
연립 방정식에서 행렬의 연산을 이끌어냈는데,
정리하면
곱셈은 교환법칙이 성립되지 않고, AB ≠ BA
결합법칙은 성립한다. (AB)C = A(BC)
분배법칙도 성립한다. (A+B)C = AC + BC
덧셈은 교환법칙과 결합법칙 모두 성립한다.
A+B=B+A, (A+B)+C = A+(B+C)
'교육 > 수알못시리즈' 카테고리의 다른 글
| 도형의 방정식 Equation of figure (0) | 2020.02.08 |
|---|---|
| 행렬의 항등원 Identity element of Matrix (0) | 2020.02.05 |
| 방정식, 다항식과 연립 방정식 훑어보기 Thumbing through equation, polynomial and system of equations (0) | 2020.02.02 |
| 실수를 선으로 나타낼 수 있는가? Can real number be expressed as a line? (0) | 2020.01.31 |
| 유리수의 n 진법 체계 n-ary numeration system of rational number (0) | 2020.01.15 |

