수학에 대해서 다른 건 기억 안나도
피타고라스 정리 이거 하나만큼은 뭔지 몰라도 기억 날 것이다.
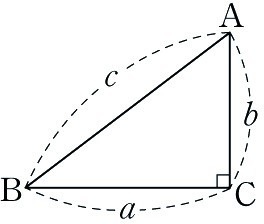
직각 삼각형이 있으면
a^2 + b^2 = c^2
이 성립한다는 것이다.
이게 워낙에 오래된 역사를 갖고 있고 유명하기까지 해서
많은 방법의 증명이 있다.
그 중에서 대표적인 증명은 4가지 정도가 된다.
아래 링크에 잘 설명되어있으니, 보면 되겠다.
피타고라스의 정리, 피타고라스의 정리 증명
학교를 졸업한 지 오랜 시간이 지난 분들도 1학기 때 공부했던 근의 공식과 이 글에서 공부할 피타고라스의 정리는 들으면 기억이 난다고 할 거에요. 피타고라스의 정리는 이처럼 학교를 졸업한 지 몇 년이 지나도..
mathbang.net
유클리드의 증명, 가필드의 증명 - 피타고라스의 정리 증명
피타고라스의 정리는 수많은 방법으로 증명이 이루어졌어요. 그중에서 가장 유명한 증명 방법인 유클리드의 증명과 가필드의 증명 방법에 대해서 알아보죠. 피타고라스의 정리, 피타고라스 정리의 증명에서도 피타..
mathbang.net
이 피타고라스의 정리를 응용해서 입체도형 대각선의 길이도 구할 수 있을 것이다.
아래 직육면체의 대각선 길이를 보도록하자.

선분 AC의 길이를 d라고하면,
d^2 = a^2 + b^2
이 된다.
그리고, 선부 AG를 f 라고 하면,
f^2 = d^2 + c^2
= a^2 + b^2 + c^2
여기에서 입체 도형의 점 간의 거리는 가로, 세로, 높이로 나타낼 수 있음을 알 수 있다.
이 사실을 좌표 공간에서 나타내면,
A를 ( x_0, y_0, z_0 ) 으로 나타내보자.
그리고, G를 ( x_1, y_1, z_1 ) 으로 나타내보자.
그러면,
a = x_1 - x_0
b = y_1 - y_0
c = z_1 - z_0
이렇게 될 것이다.
그러면 선분 AG 길이 제곱은
a^2 + b^2 + c^2 이므로
( x_1 - x_0 ) ^2 + ( y_1 - y_0 )^2 + ( z_1 - z_0 )^2
이 될 것이다.
공간에서의 점 간의 거리는 각 축 좌표의 차이의 제곱의 합으로 나타낼 수 있다는 얘기다.
이 정리를 n개의 수직한 축으로 된 n차원 공간으로도 확장시킬 수 있을 것이다.
수직한 선분끼리는 피타고라스 정리를 쓸 수 있으며,
축이 n 개이므로, n개 방향의 선분의 길이를 이용하여 길이를 구할 수 있으므로
피타고라스 정리에서의 항의 개수는 n개가 될 것이다.
두 점
이 있다고 하자.
저기 위에서 R^n은 n 차원 공간이란 뜻이다.
기호의 조합은 두 점이 n차원 공간에 있다는 뜻이고 말이다.
이때, 두 점간의 거리는
이렇게 나타낼 수 있다.
저기 위에서 R^n은 n 차원 공간이란 뜻이다.
'교육 > 수알못시리즈' 카테고리의 다른 글
| 삼각형에서의 사인, 코사인 정리 Theorem about sine and cosine in triangle (0) | 2020.02.17 |
|---|---|
| 피타고라스 삼조 Pythagorean triple (0) | 2020.02.17 |
| 삼각형과 사각형의 넓이 Area of triangle and quadrangle (0) | 2020.02.14 |
| 삼각비와 삼각함수 Triangle ratio and trigonometric functions (0) | 2020.02.11 |
| 도형의 방정식 Equation of figure (0) | 2020.02.08 |




